实验成果简介
本小组此次实验中在流水线 CPU 的基础上,增加拓展了以下内容:
-
RV32I 指令集补全(37 条),RV32IC 压缩指令拓展(26 条)
-
采用两级动态 Branch History Table 分支预测
-
支持 L1d Cache,并调整存储结构
-
对于 0x00000000 至 0x000003ff,作为常用内存区域,与 VGA 共享内存
(这一部分相当于始终不会被换出的 cache)
- 0x0000ff00 至 0x0000ffff 是 MMIO 区域
- 其余部分使用 L1d cache 连接主存,总共使用 BRAM 16KB(16 千字节)
-
-
提供可以实际运行的生命游戏,井字棋和贪吃蛇程序
- 使用 C 语言编写程序,探索了交叉编译流程,增进了对计算机抽象层级的理解
- 增添了对 VGA 屏幕外设的使用,使得程序更具有表现力
- 考虑了一般性的外设拓展方法
- 一般地,对数据寄存器封装,使用 MMIO
- 特别地,由于 VGA 模块数据需求量较大,采取了共享内存的方式
项目仓库:https://github.com/liuly0322/ustc-codh-lab6
实验环境
- Vivado 2019.1
- Verilator 4.220
指令集扩充
实现所有 RV32I 指令(37 条):
- add, sub, and, or, sll, sra, srl, xor, slt, sltu
- addi, andi, ori, slli, srai, srli, xori, slti, sltiu
- auipc, lui
- lw, sw, lb, lbu, lh, lhu, sb, sh
- beq, bne, blt, bge, bltu, bgeu
- jal, jalr
实现所有 RV32IC 压缩指令(26 条):
- c.nop
- c.add, c.addi, c.addi16sp, c.addi4spn, c.and, c.andi, c.slli, c.srai, c.srli, c.sub, c.mv, c.or, c.xor
- c.j, c.jal, c.jr, c.jalr, c.beqz, c.bnez
- c.li, c.lui, c.lw, c.lwsp, c.sw, c.swsp
RV32IC 是 RV32I 对应的压缩指令集,允许极大节省编译出程序的空间
原理介绍
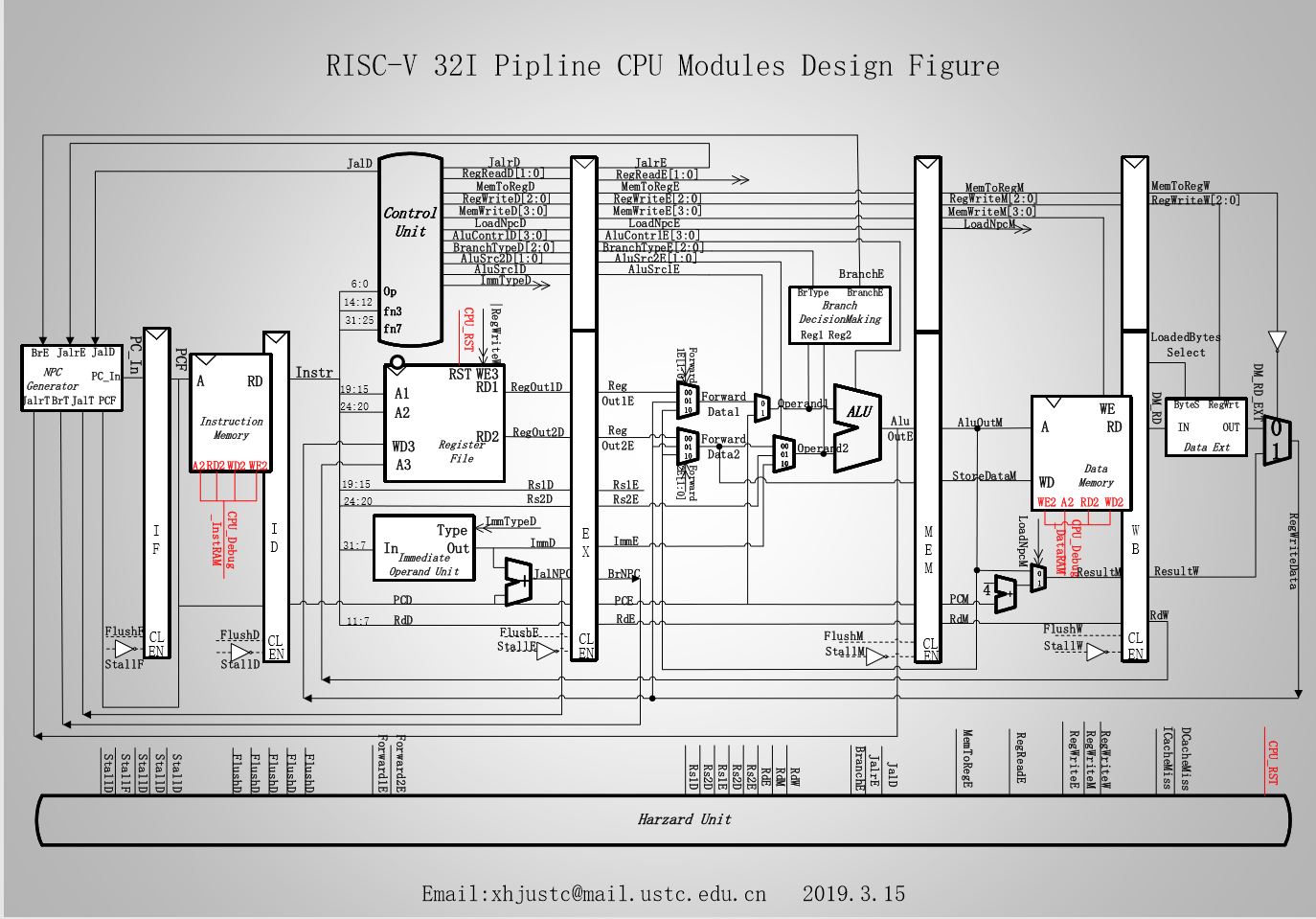
整体数据通路参考:
下面具体介绍一些涉及到的修改:
-
ALU 和 control 模块修改
对于置位指令,lui 指令,可以和算数逻辑指令统一,让写回寄存器的数据来源取 ALU 输出,通过控制 ALU 操作数让 ALU 计算出正确的结果
module alu #( parameter AW = 5, parameter DW = 32) (input [DW - 1: 0] a, input [DW - 1: 0] b, // 两操作数 input [3: 0] s, // 功能选择 output reg [DW - 1: 0] y, // 运算结果 output [2: 0] f); // 标志 // 大小判断 wire [DW - 1: 0] a_minus_b = a - b; wire a_s = a[DW - 1]; wire b_s = b[DW - 1]; wire y_s = a_minus_b[DW - 1]; // 移位 wire [AW - 1: 0] b_shift = b[AW - 1: 0]; // 大小比较信号 wire less_signed = (a_s & ~b_s) | (a_s & y_s) | (~b_s & y_s); wire less_unsigned = (~a_s & b_s) | (~a_s & y_s) | (b_s & y_s); assign f = {less_unsigned, less_signed, (a_minus_b == 0)}; always @(*) begin case (s) 4'b0001: y = a_minus_b; 4'b0010: y = a & b; 4'b0011: y = a | b; 4'b0100: y = a ^ b; 4'b0101: y = a >> b_shift; 4'b0110: y = a << b_shift; 4'b0111: y = ($signed(a)) >>> b_shift; // signed 4'b1000: y = {31'b0, f[1]}; 4'b1001: y = {31'b0, f[2]}; 4'b1010: y = b; default: y = a + b; endcase end endmodule可以看到,
4'b1000和4'b1001用于置位指令,4'b1010用于 lui这样修改最大程度保持了数据通路的简洁性
控制模块根据指令 funct3 位的值生成 ctrl_alu_op 信号
-
跳转判断和访存指令都需要用到 funct3 位,可以直接流水段传递
对于跳转指令,有:
- funct3[2],用于区分使用 alu 的相等判断还是大小比较
- funct3[1],用于区分如果比较大小,是否使用无符号数
- funct3[0],用于区分功能相反的跳转指令,例如 beq 和 bne
因此 EX 段判断是否应该跳转的逻辑如下:
wire should_branch = funct3_ID[0] ^ (!funct3_ID[2]? alu_f[0]: ((funct3_ID[1] == 1)? alu_f[2]: alu_f[1]));对于访存指令,类似地区分 lw, sw, lb, lbu, lh, lhu, sb, sh 即可
-
新增压缩指令集
出于时序考虑,IF 段只需要判断当前 ir 是不是压缩指令来决定下一条 pc
wire [31:0] pc_2 = pc + 32'h2; wire [31:0] pc_4 = pc + 32'h4; wire is_compressed = pc[1] || (ir[1:0] != 2'b11); always @(posedge clk) begin ...... // 其他跳转逻辑 else if (is_compressed) pc <= pc_2; else pc <= pc_4; endID 段增加压缩指令到完整指令的译码:
wire is_compressed = pc_IF[1] || (ir_IF[1:0] != 2'b11); wire [15:0] ir_compressed = pc_IF[1]? ir_IF[31:16]: ir_IF[15:0]; wire [31:0] ir_dec; wire [31:0] ir = is_compressed? ir_dec: ir_IF; decompression u_decompression( .IF_Instr_16 ( ir_compressed ), .IF_Dec_32 ( ir_dec ) );给出的 ir 作为实际译码的指令
代码的解压缩模块参照每条压缩指令具体的说明即可,具体可以见本项目源码
新增指令测试
对新增的指令进行了较为充分的测试:
 |
 |
 |
|---|---|---|
| 新增 R 型和 I 型指令 | 访存指令测试 | 压缩指令测试 |
加上原有的 10 条指令的功能测试及 bypass 测试,总共使用了 181 个测试样例
测试原理示例:
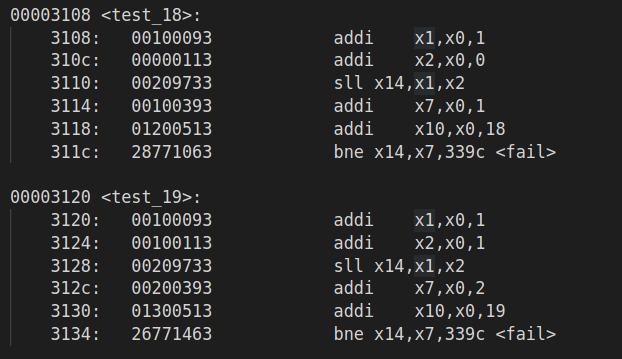 |
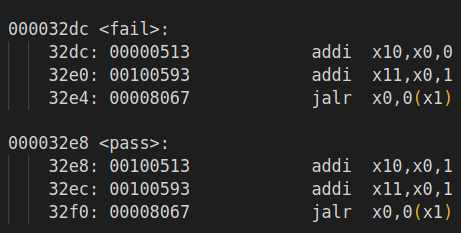 |
|---|---|
| 具体案例用 x10 计数 | x11 表示结束,此时 x10 存储结果 |
可以在仿真过程中,读 x11 和 x10 寄存器,来获取当前进行到了第几个测试样例,以及相应通过情况
对应仿真程序:
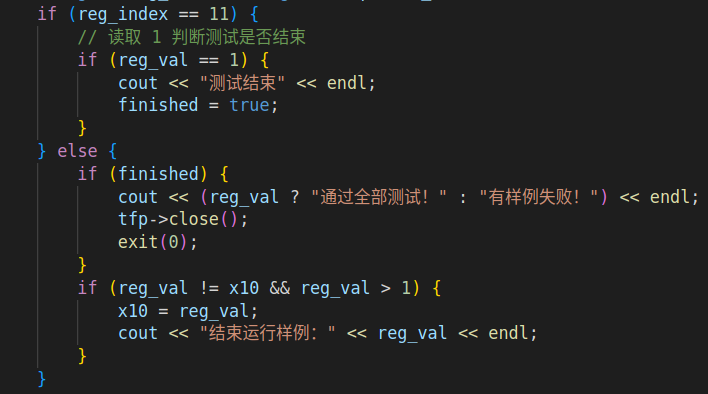
Verilator 高级语言仿真
简介
Verilator 是一款高性能的 Verilog/System Verilog 开源仿真工具。运用 Verilator package,我们可以将 Verilog 和 System Verilog HDL 语言设计编译转换成 C++ 或者 SystemC 模型,所以从这个意义上来说,Verilator 更应该被成为是一个编译器而不是一个传统意义上的仿真器。
通常情况下,Verilator 的工作流程如下所示:
- 首先 Verilator 将读取特定的 HDL 文件并检查其代码,同时还可以选择支持检查覆盖率和 debug 波形的生成。然后将源文件编译成源代码级的
C++或SystemC模型。其输出的模型会以.cpp和.h文件存在。 - 为了能够完成仿真,额外需要一个用户自行编写的 C++ wrapper,这个 wrapper 与传统的 Verilog Testbench 功能类似,主要是为了连接顶层模块,并给予相应的激励。
- 在 C++ 编译器的工作下,所有的之前生成的文件(C++ wrapper 以及 Verilated Model)以及库文件(Verilator 提供的 runtime library 或者 SystemC 库文件)会被一同合并成一个可执行文件。
- 执行生成的可执行文件,就可以开始实际的仿真,”simulation runtime”
优势
- 最快的开源仿真器
- coverage test(覆盖测试)
- 覆盖率,便于功能验证
- 断言式的测试样例(灵活度高),对应 Verilog testbench 文件中的 function 或者 task,但编写起来更为容易,可以自动判断 CPU 功能正确与否
|  |
|  |
| ————————– | ————————– |
|
| ————————– | ————————– |
图:覆盖测试能解决的痛点
存储结构及一级数据 Cache
本实验更改了原先存储结构
-
对于 0x0000 至 0x3ffff,作为常用内存区域,与 VGA 共享内存
这一部分相当于始终不会被换出的 cache
-
0xff00 至 0xffff 是 MMIO 区域
-
其余部分使用 L1d cache 连接主存,总共使用 BRAM 16KB(16 千字节)
这一部分可以通过组合逻辑对内存进行封装:
reg [31:0] mem_in; // 写入数据寄存器的数据
wire [31:0] shared_out, cache_out;
wire [31:0] mem_out; // 数据存储器读出的 32 位数据
reg [31:0] mdr; // 实际返回的数据
wire is_mmio = (a[31:8] == 24'h0000ff); // 判断现在是主存还是 mmio
wire is_shared = (a[31:8] < 4); // 共享内存区域
wire is_cache = ~is_shared & ~is_mmio;
assign spo = is_mmio? io_din : mdr;
assign mem_out = is_shared? shared_out: cache_out;
本实验中的 Cache 采用直接映射 + 写回 + 写分配策略,具体状态机如下图所示:
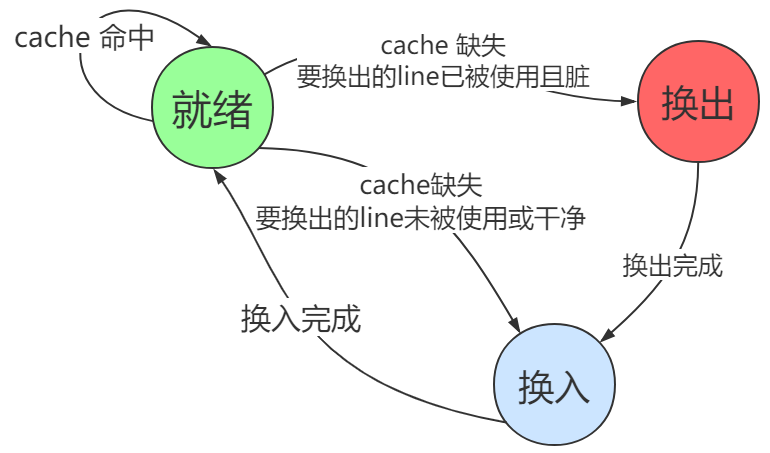
Cache 代码及可综合的 BRAM 代码参考:https://github.com/Summer-Summer/ComputerArchitectureLab
本实验 Cache 规格:
tag 6 位,index 3 位,偏移 5 位(3 位字偏移)
增添上 Cache 后,需要对原先的 hazard 处理模块也进行相应的更改
module hazard(
input rstn,
input miss,
input pc_change_EX,
input load_use_hazard,
output stall_IF,
output stall_ID,
output stall_EX,
output flush_IF,
output flush_ID
);
assign stall_IF = load_use_hazard | miss;
assign stall_ID = miss;
assign stall_EX = miss;
assign flush_IF = rstn & pc_change_EX;
assign flush_ID = rstn & (pc_change_EX | load_use_hazard);
endmodule
在 Cache Miss 时,需要阻塞流水线的各个段间寄存器
功能测试
为了验证我们 Cache 功能是否正常,这里编写了下述测试程序:
// MMIO: 8'h0c: 数码管输出
int fib_ans[200] = {1, 1};
int fib(int x) {
volatile unsigned* p = 0xff0c;
if (fib_ans[x]) {
return fib_ans[x];
}
int ret = fib(x-1) + fib(x-2);
fib_ans[x] = ret;
*p = ret;
return ret;
}
int main() {
fib(200);
}
依次计算斐波那契数列,并将结果输出到数码管
编译后得到:
3020: ff010113 addi x2,x2,-16
......
3080: 01010113 addi x2,x2,16
3084: 00008067 jalr x0,0(x1)
可以看到,在递归计算时会用到栈指针 sp ,我们可以在计算过程中记录 sp 的最小值,仿真程序:
int a = 1, b = 1, cnt = 0;
unsigned min_stack = 0xffffffff;
while (!Verilated::gotFinish() && main_time < sim_time) {
// 循环读取内存值
top->clk = !top->clk;
top->eval(); // 仿真时间步进
tfp->dump(main_time); // 波形文件写入步进
if (top->io_we) {
int data = top->io_dout;
if (data != b) {
b = a + b;
a = b - a;
if (data != b) {
cout << "失败:计算 fib 预期" << b << endl;
}
cnt++;
cout << "预期" << b << " 实际" << data << endl;
if (cnt > 190) {
cout << "通过 fib 测试" << endl;
cout << std::hex << "最小栈地址:" << min_stack << endl;
tfp->close();
exit(0);
}
}
}
if (top->chk_data < min_stack && main_time > 200) {
min_stack = top->chk_data;
}
main_time++;
}
实际运行,得到结果:
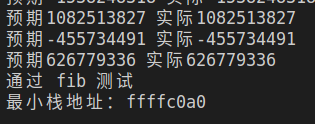
注意栈地址从 0xffffffff 到 0xffffc0a0,后 14 位从 0x3fff 遍历到 0x00a0 ,几乎取遍了主存,可见在入栈出栈过程中 cache 进行了正确的换入换出
分支预测
意义
根据 Real Silicon 调研的数据,对于现代编译器编译后的程序,大概每隔 4.6 - 5.2 条指令就有一个分支(包括 call 和 direct jump 这种非条件分支),而在我们的五级流水线 CPU 上,每次挑战失败都需要损失两个周期,相当于执行了两条空指令,也就是说,在分支预测完全失败的情况下,不考虑其他相关引起的流水线停顿,我们的 CPU 的 CPI 已经高达 1.4,如果能够通过分支预测的方式将 CPI 降低到 1 左右,就可以提高约 40% 的性能,这是一个很诱人的数字。下面,将首先介绍几种分支预测策略的原理,再给出本组的实现
原理
主要分为静态分支预测和动态分支预测两类。
静态分支预测
- 预测统一不跳转 / 统一跳转
- 取下一条指令统一发射地址较小的
- ……
动态分支预测
-
缓存跳转后地址,并且用 1bit 记录上次分支的结果(BTB)
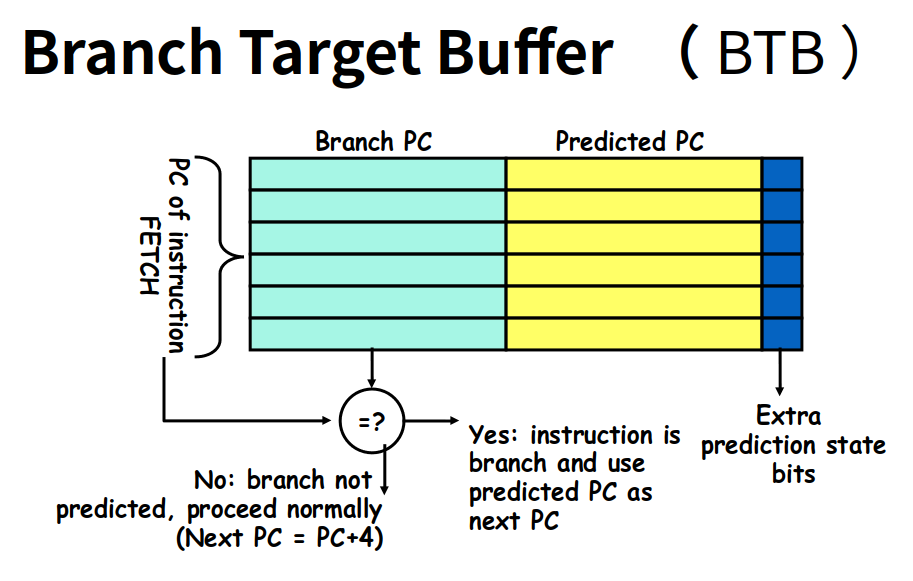
-
基于两位饱和计数器的分支预测 (BHT)
这种方式是在 BTB 基础之上的改进,仍然需要 BTB 表,但是判断某分支是否跳转的依据不再是 1bit 的上一次记录,而是为每个分支指令映射到一个 2bit 的饱和计数器上,这样抗干扰能力更强(当之前连续跳转失败时,只有连续两次跳转成功才能使状态机变为预测跳转的状态,同理,如果连续跳转成功,那么需要连续两次跳转失败才能使状态机给出的预测变为不跳转)

-
两级适应性训练 Two-Level Adaptive Training
- 提出:Tse-Yu Yeh 和 Yale N. Patt
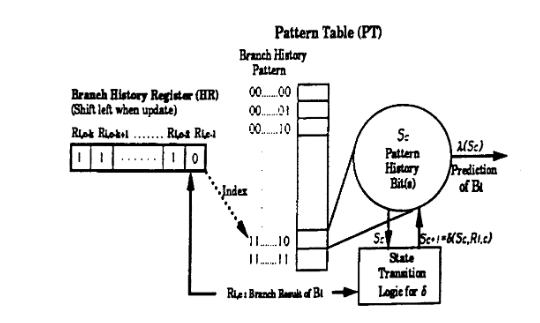
在 BHT 的基础上改进,对于 每个分支指令跳转的 pattern(模式) 都映射到一个饱和计数器,进一步提高了分支预测准确性
例如,如果一个分支指令跳转与否的历史记录分别是:
TNNNTNNNTNNNTNNN...那么,分支预测器就会学习到,如果前几次的 pattern 是
TNNN,则下一次预测结果应该是T,因为TNNN这一模式对应的饱和计数器可以被学习为预测跳转的状态这对于以下的跳转模式十分有用:
for (int i = 0; i < n; i++) { if (i % 4) { // do something } // do something }if指令跳转与否具有周期性,可以被记忆
值得注意的是,动态分支预测和静态分支预测并不是对立的,对于某条跳转指令,在第一次执行到时,动态分支预测可以采用静态预测的方法给出它跳转与否的初值,进一步提高预测准确性
Verilog 实现
采用 BTB + 2-level adaptive training 的策略
对应流程图:
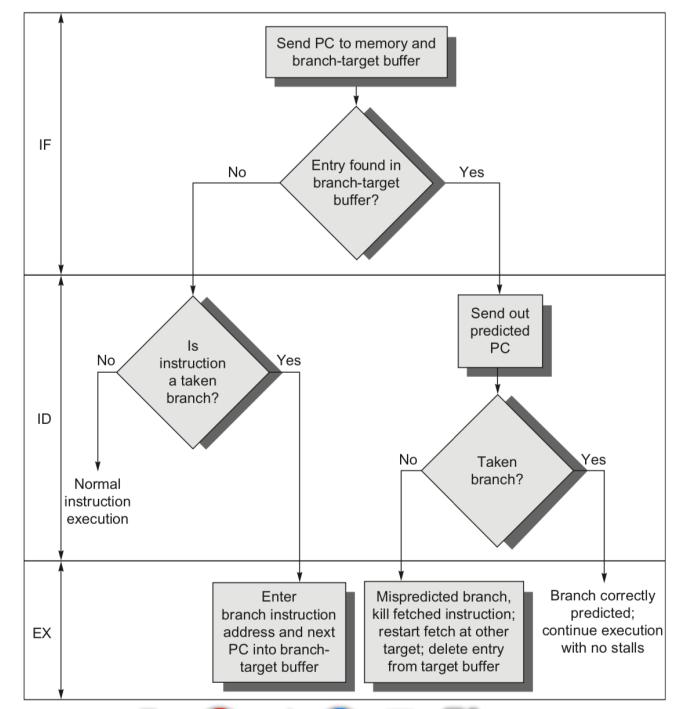
IF 段如果 PC 被预测跳转,下一个周期 PC 可以直接变为从 BTB 表中读出的跳转后 PC
同时,预测跳转与否的信息也会沿着流水线传递到 EX 段,EX 段根据实际跳转与否,可能需要将跳转后 PC 写入 BTB 表,并通知分支预测模块更新饱和计数器
整体模块如下所示:
module branch_predict(
input clk,
input rstn,
// EX 段记录结果
input record_we, // 是否记录分支历史
input [9:2] record_pc, // 记录的 pc
input record_data, // 记录是否跳转
input [31:0] record_pc_result, // 记录跳转后 pc
// IF 段查询当前 pc
input [9:1] chk_branch_pc,
output predict, // 预测结果
output [31:0] predict_pc // 预测的 pc
);
reg [31:0] btb[0:255]; // BTB 表
reg [1:0] record[0:255]; // (hash 后) 饱和计数器
reg [2:0] history[0:31]; // (hash 后) 分支历史
wire [4: 0] chk_pc_hash = chk_branch_pc[6:2];
wire [4: 0] record_pc_hash = record_pc[6:2];
// 预测 pc 只取 [9:2],所以如果是高位压缩指令,直接不预测,返回 0
assign predict_pc = btb[chk_branch_pc[9:2]];
assign predict = !chk_branch_pc[1] & rstn & (查询 record 应该跳转) & (predict_pc != 0);
always @(posedge clk) begin
if (record_we) begin
// 记录跳转后地址
if (record_data) begin
btb[record_pc] <= record_pc_result;
end
// 指令对应的跳转历史左移一位
history[record_pc_hash] <= {history[record_pc_hash][1:0], record_data};
// 下面判断是否需要更新饱和计数器
......
end
end
endmodule
IF 段:
always @(posedge clk) begin
if (!rstn)
pc <= 32'h3000;
else if (pc_change_EX)
pc <= pc_nxt_EX;
else if (stall_IF)
pc <= pc;
else if (predict) // 如果预测跳转
pc <= predict_pc;
else if (is_compressed) // 不跳转或不预测跳转,按照正常逻辑更新 pc 即可
pc <= pc_2;
else
pc <= pc_4;
end
EX 段:
always @(*) begin
if (ctrl_jal_ID | ctrl_jalr_ID)
pc_nxt_EX = alu_out;
else if (pc_branch_EX && predict_ID && !should_branch) // 预测跳转但没有跳转
pc_nxt_EX = pc_4_ID;
else // 预测不跳转但跳转
pc_nxt_EX = pc_ID + imm_ID;
end
assign record_we = ctrl_branch_ID | jal_fail;
assign record_data = ctrl_jal_ID? 1: should_branch;
assign record_pc_result = pc_nxt_EX;
这里我们也将 jal 跳转后地址存入 BTB 表,使得 jal 指令的跳转后地址也可以在 EX 段计算出
hazard 模块:
......
assign flush_IF = rstn & pc_change_EX;
assign flush_ID = rstn & (pc_change_EX | load_use_hazard);
可以看到预测失败的代价是两个周期
下面分别挑选排序测试以及两个分支测试样例,对比采用不同的分支预测策略对性能的提高情况
排序测试
对内存中的 16 个数进行冒泡排序
.data
...... # 这里有 16 个数
.text
addi t1, zero, 0 # sorted
addi t0, zero, 17 # set n to array size + 1
addi a1, zero, 16 # const size (for print out
addi a0, zero, 1 # const 1
OUTER:
addi t0, t0, -1
sub t1, a0, t1
beqz t1, END
addi t2, zero, 0 # i = 0
INNER:
addi t2, t2, 1 # init: i = 1
beq t2, t0, OUTER
addi t5, t2, -1
add t5, t5, t5
add t5, t5, t5
lw t3, (t5)
add t6, t2, t2
add t6, t6, t6
lw t4, (t6)
blt t3, t4, INNER
beq t3, t4, INNER # 否则需要交换
sw t3, (t6)
sw t4, (t5)
addi t1, zero, 0
j INNER
END:
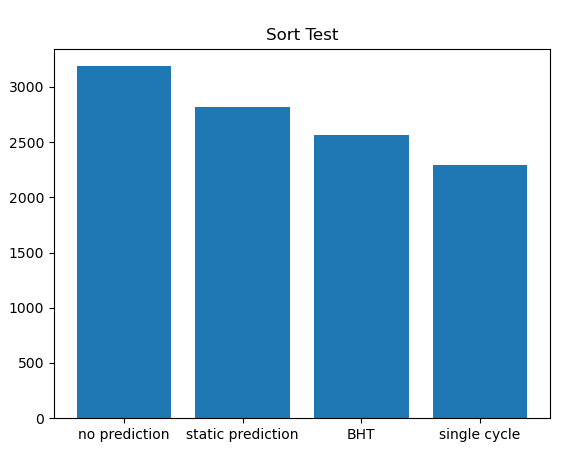
对几种分支预测方式进行测试:
| 单周期 | 无分支预测 | 静态分支预测 | BTB 预测 | |
|---|---|---|---|---|
| 周期 |  |
 |
 |
 |
| CPI | 1 | 1.392 | 1.231 | 1.119 |
对于排序比较的随机跳转,静态分支预测和 BTB 预测差距不大,BTB 主要提升了用于循环的跳转语句预测成功率
可以看到,BTB 预测和单周期的基准大约只差了 10%
这里由于排序结果导致的跳转比较随机,两级适应性 BHT 和 BTB 结果差距不大,不再列出
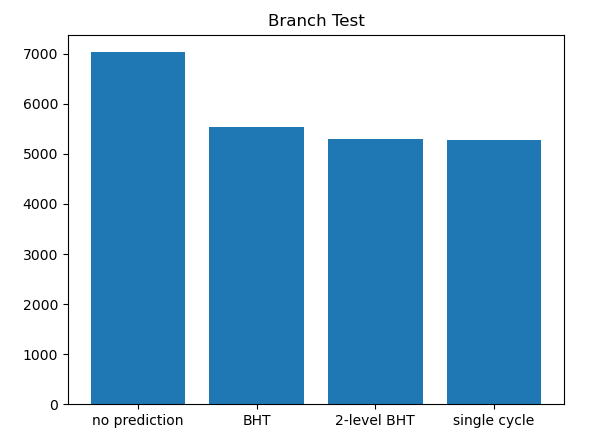
分支测试
这一组测试主要体现两级适应性 BHT 对分支历史 pattern 的学习能力
for (int i = 0; i <= 1000; i++) {
if (i % 4 == 0) {
i+= 4;
}
}
汇编:
addi a0, zero, 1000
addi t0, zero, 0 # a
addi t1, zero, 0 # i
LOOP:
blt a0, t1, FINISH
andi t2, t1, 3
bnez t2, CONT
addi t1 t1, 4
CONT:
addi t1, t1, 1
j LOOP
FINISH:
addi t6, zero, 1
对几种分支预测方式进行测试:
| 单周期 | 无分支预测 | BHT | 两级 BHT | |
|---|---|---|---|---|
| 周期 |  |
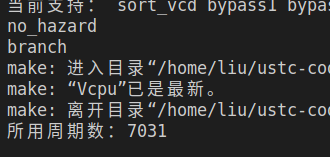 |
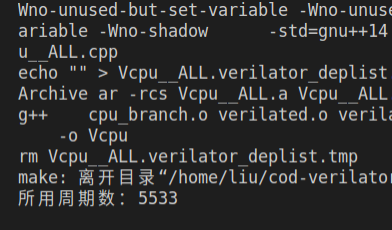 |
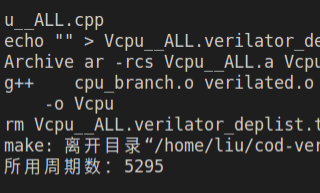 |
| CPI | 1 | 1.333 | 1.049 | 1.004 |
两级 BHT 在这种情况下将 CPI 几乎降低到了 1,相比 BHT 进一步提高了准确率
实际应用测试
这里实际搭载了 gcc 编译出的贪吃蛇程序(具体见下文),进行了分支预测性能和准确率的测试
在 ID 段统计总指令数:
reg [31:0] instr_cnt;
always @(posedge clk) begin
if (!flush_ID && ir_IF != 0)
instr_cnt <= instr_cnt + 1;
end
在 EX 段统计跳转指令和 jal 的次数,并统计跳转失败的发生:
reg [31:0] is_branch_cnt, fail_cnt, is_jal_cnt;
always @(posedge clk) begin
if (ctrl_branch_ID)
is_branch_cnt <= is_branch_cnt + 1;
if (ctrl_jal_ID)
is_jal_cnt <= is_jal_cnt + 1;
if (pc_branch_EX || jal_fail)
fail_cnt <= fail_cnt + 1;
end
因为 PDU 模块为了真实上板做了降频,取边沿等处理,对于模拟 I/O 交互不是很友好,如果对 top 模块整体仿真,往往需要连续仿真几毫秒甚至几十毫秒以上,仿真速度较慢,因此这里采用 Verilator 模拟 PDU 模块的功能
top 文件:
module top_test(
input clk, // clk100mhz
input rstn, // cpu_resetn
output [31:0] pc,
// for simulate io
output [7:0] io_addr,
output io_rd,
input [31:0] io_din
);
wire [31 : 0] io_dout;
wire io_we;
wire [31 : 0] chk_data;
wire [31:0] vga_data;
cpu CPU (.clk(clk), .rstn(rstn), .vga_addr(0), .vga_data(vga_data),
.io_addr(io_addr), .io_dout(io_dout), .io_we(io_we),
.io_rd(io_rd), .io_din(io_din),
.pc(pc), .chk_addr(0), .chk_data(chk_data));
endmodule
仿真文件:
srand((unsigned)time(NULL));
int swx_data = rand();
cout << swx_data;
int end_cnt = 0;
int prev_pc = 0;
while (!Verilated::gotFinish()) {
// 循环读取内存值
if (top->io_rd) {
int addr = top->io_addr;
if (addr == 0x18) {
top->io_din = main_time;
} else if (addr == 0x10) {
top->io_din = 1;
} else if (addr == 0x14) {
top->io_din = swx_data;
} else {
top->io_din = 0;
}
} else {
top->io_din = 0;
}
if (top->pc == prev_pc) {
end_cnt++;
} else {
end_cnt = 0;
}
if (end_cnt == 100) {
break;
}
prev_pc = top->pc;
top->clk = !top->clk;
top->eval(); // 仿真时间步进
tfp->dump(main_time); // 波形文件写入步进
main_time++;
}
这里模拟了游戏开始后,利用开关,随机给游戏输入一个种子 swx_data ,之后,贪吃蛇会吃掉它面前的苹果,CPU 上运行的程序再根据开关输入的随机数种子,生成下一个苹果所在的位置。接下来,贪吃蛇会一直向下撞到边界,游戏结束
可以看到,该测试环境模拟了贪吃蛇程序的主要流程,具有较好的代表性
原先程序需要轮询等待计时器,显然会极大提高分支预测准确率,这里对汇编进行了修改,去除了等待计数器,排除了这一因素的干扰
下面观看波形,记录五组数据的结果:
| 组 1 | 组 2 | 组 3 | 组 4 | 组 5 | |
|---|---|---|---|---|---|
| 种子 | 168024705 | 481046883 | 482655648 | 817451524 | 1428754955 |
| jal | 0x510 | 0x511 | 0x4c4 | 0x514 | 0x52c |
| jal 失败 | 0x29 | 0x29 | 0x0e | 0x29 | 0x2e |
| branch | 0x1e08 | 0x1ec8 | 0x2025 | 0x207c | 0x2164 |
| branch 失败 | 0xae | 0xb0 | 0xa7 | 0xb6 | 0xbd |
| branch 预测率 | 97.74% | 97.77% | 97.97% | 97.81% | 97.79% |
| 整体预测率 | 97.61% | 97.64% | 98.08% | 97.68% | 97.62% |
| 总指令数 | 0x9cb4 | 0x9f57 | 0xb866 | 0xa556 | 0xa860 |
| 总周期数 | 43046 | 43725 | 50220 | 45272 | 46074 |
| CPI | 1.073 | 1.072 | 1.064 | 1.070 | 1.069 |
| 无分支预测 CPI | 1.510 | 1.511 | 1.456 | 1.513 | 1.516 |
| 性能提升 | 40.7% | 41.0% | 36.8% | 41.4% | 41.8% |
可以看到,我们采取的分支预测策略使得整体预测准确率达到 97% 至 98% 左右,带来了约 40% 的性能提升
生命游戏
作为示例,本 cpu 搭载了三个和 vga 结合的展示程序,分别是生命游戏,井字棋和贪吃蛇
编译
首先简单介绍一下这三个程序的编译环境
使用 vlab 提供的 riscv 交叉编译工具链,使得仅需要编写 C 程序就可以很方便的烧写上板
环境如下:
- Vlab Ubuntu 20.04
- riscv32-unknown-elf-gcc 10.2.0
参考修改助教 makefile ,自动生成 objdump 等文件,便于仿真及上板测试
这里需要注意的是,如果编译开启了 -O2 优化选项,那么一些对于 MMIO 区域的数据读写操作可能会因为编译器优化而消失,导致 CPU 并未如预期读写这些地址,甚至发生死循环。可以考虑在 C 程序中对 MMIO 地址添加 volatile 关键词来禁止编译器的这一优化
简介
生命游戏中,对于任意细胞,规则如下:
- 每个细胞有两种状态 - 存活或死亡,每个细胞与以自身为中心的周围 八格 细胞产生互动(如图,黑色为存活,白色为死亡)
- 当前细胞为存活状态时,当周围的存活细胞低于 2 个时,该细胞变成死亡状态。(模拟生命数量稀少)
- 当前细胞为存活状态时,当周围有 2 个或 3 个存活细胞时,该细胞保持原样。
- 当前细胞为存活状态时,当周围有超过 3 个存活细胞时,该细胞变成死亡状态。(模拟生命数量过多)
- 当前细胞为死亡状态时,当周围有 3 个存活细胞时,该细胞变成存活状态。(模拟繁殖)
可以把最初的细胞结构定义为种子,当所有在种子中的细胞 同时 被以上规则处理后,可以得到第一代细胞图。按规则继续处理当前的细胞图,可以得到下一代的细胞图,周而复始。
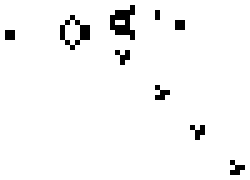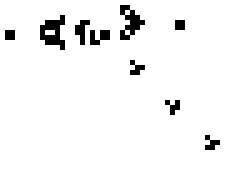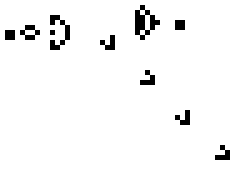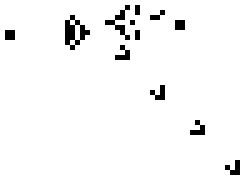
C 语言实现
-
插入 nop 模拟定时
for (int i = 0; i < 2000000; i++) { asm("addi x0,x0,0"); } -
状态压缩 + 位运算
if (life[x] & (1 << y)) { state[x] += (cnt == 2 || cnt == 3)? (1 << y) : 0; } else { state[x] += (cnt == 3)? (1 << y) : 0; }
VGA 驱动
这里采用的是共享内存的方式,VGA 可以访问主存中的数据从而进行显示器 RGB 信号的映射
graph LR
cpu--read/write-->memory
vga_output---vga_driver--read-->memory
展示
稳定的 “脉冲星” 图形(周期为 3)

详细视频:http://home.ustc.edu.cn/~liuly0322/videos/life_game.mp4
井字棋
C 语言实现
#define input_flag 0xff10
#define input_data 0xff14
......
if (!(*((unsigned int*)input_flag))) {
continue;
}
// 用户输入的值:1-9,表示下在哪个格子
unsigned int user_input = (*((unsigned int*)input_data));
// 判断下的位置是否合法
if (!user_input || user_input > 9 || state[user_input - 1])
continue;
state[user_input - 1] = turn;
cnt++;
// 首先判断是否胜利,再判断是否占满
if (state[0] == turn && state[1] == turn && state[2] == turn ||
state[3] == turn && state[4] == turn && state[5] == turn ||
state[6] == turn && state[7] == turn && state[8] == turn ||
state[0] == turn && state[3] == turn && state[6] == turn ||
state[1] == turn && state[4] == turn && state[7] == turn ||
state[2] == turn && state[5] == turn && state[8] == turn ||
state[0] == turn && state[4] == turn && state[8] == turn ||
state[2] == turn && state[4] == turn && state[6] == turn) {
// 胜利
state[9] = turn;
} else if (cnt == 9) {
state[9] = 0;
}
// 圈和叉转换
turn = 3 - turn;
}
// 死循环等待结果输出
while (1)
;
从中可以看到交叉编译的方便之处
展示
不同的胜负画面:
|  |
|  |
|  |
| ————————– | ————————– | ————————- |
|
| ————————– | ————————– | ————————- |
详细视频:http://home.ustc.edu.cn/~liuly0322/videos/tic_tac_toe.mp4
贪吃蛇
外设使用
贪吃蛇可以比较好的体现出 CPU 处理外部设备的能力
此程序通过 MMIO ,需要访问:
- 性能计数器,起到一个计时器的功能
- 上下左右按钮的输入
- 硬件随机数发生器(可选)
本程序采用初始种子生成苹果坐标,故没有采用硬件随机数生成器;通过轮询的方式,与性能计数器和按钮输入达成了良好的交互
从中也可以看出,中断对于外设交互并不是必须的
最初引入硬件中断,只是出于性能上的考量。如果电脑系统没有中断,则处理器与外部设备通信时,它必须在向该设备发出指令后进行忙等待(Busy waiting),反复轮询该设备是否完成了动作并返回结果。这就造成了大量处理器周期被浪费。引入中断以后,当处理器发出设备请求后就可以立即返回以处理其他任务,而当设备完成动作后,发送中断信号给处理器,后者就可以再回过头获取处理结果。这样,在设备进行处理的周期内,处理器可以执行其他一些有意义的工作,而只付出一些很小的切换所引发的时间代价
C 语言实现
while (1) {
// 等待计时器
if ((int)get(CNT_DATA) - past_time < interval) {
continue;
}
past_time += interval;
// 确认当前方向
if (get(BTN_VLD))
direction = get(BTN_DATA);
// 之前的蛇头变为蛇身
set(head_x, head_y, BODY_BASE + direction);
// 计算更新后蛇头坐标
if (direction == UP) {
head_x -= 1;
} else if ......
// 如果吃到苹果,更新苹果坐标,否则移动蛇尾
if (head_x == apple_x && head_y == apple_y) {
set(head_x, head_y, NONE);
// 随机生成新的坐标
......
set(apple_x, apple_y, APPLE);
} else {
int tail_direction =
((snake[tail_x][tail_y >> 3] >> (tail_y << 2)) & 15) -
BODY_BASE;
set(tail_x, tail_y, NONE);
// 更新 tail 的位置
......
}
// 苹果处理完之后,如果当前蛇头所在格子不为空,则说明碰到障碍,退出
int head_state = (snake[head_x][head_y >> 3] >> (head_y << 2)) & 15;
if (head_state != NONE)
break;
// 设置蛇头,等待下个循环的计算
set(head_x, head_y, HEAD);
}
状态编码采用宏定义配合状态压缩
// 状态压缩,30 行,40 列,8 列压缩为一个 int(32 位)
// 对应每个格子 4bit,参考 00(R分量)0(G分量)0(B分量)
#define NONE 0 // 空格
#define BORDER 1 // 蓝色边框
#define HEAD 2 // 绿色蛇头
#define APPLE 4 // 红色苹果
#define BODY_BASE 7
#define BODY_L 9 // 蛇身,左
#define BODY_R 8 // 蛇身,右
#define BODY_U 15 // 蛇身,上
#define BODY_D 11 // 蛇身,下
// 对应 rv32i 的 lw 指令
inline unsigned get(int p) {
return *((unsigned*)p);
}
// 输入需要设置的坐标和状态
inline void set(unsigned x, unsigned y, unsigned state) {
// 先抹平这些位,再将数据移位
snake[x][y >> 3] &= (~(15 << (y << 2)));
snake[x][y >> 3] |= (state << (y << 2));
}
展示
有较好的操作感

详细视频:http://home.ustc.edu.cn/~liuly0322/videos/snake.mp4
持续集成
出于项目完整性考虑,使用 Github Actions,增添了自动的持续集成测试
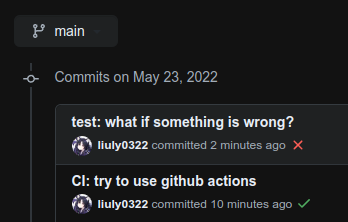 |
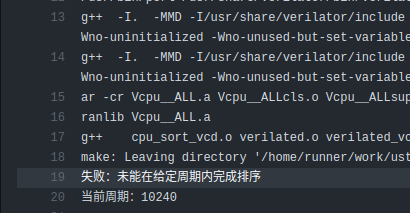 |
|---|---|
| Push 后自动运行测试 | 具体错误信息提示 |
测试脚本和 github actions 的 yml 文件具体参见本项目仓库
致谢
- 感谢老师和助教们一个学期以来的辛苦付出
- 本项目得到了中国科学技术大学 Vlab 实验平台的帮助与支持
- 自动化测试参考